电工学/电路 - 结点电压法

节点电压法 (文章) | 直流电路分析 | 可汗学院 (khanacademy.org)

MITx 的做法：

1. 选取接地点
2. 用$e_k$标出除接地点外的结点电位
3. 对每个结点列KCL方程
4. 求解方程并求其他量

例题

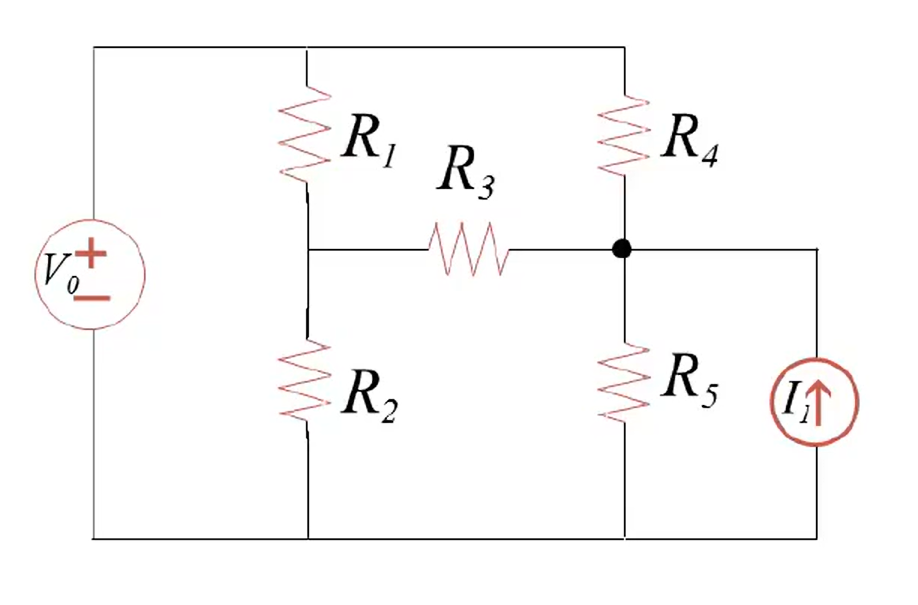
选取接地点

选择连接元件最多的那个结点或连接电压源负极的结点
此处为

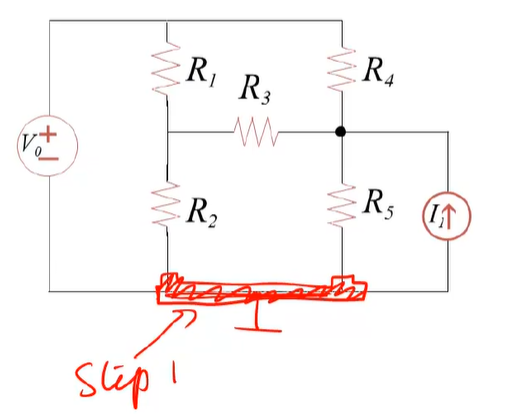
用$e_k$标出除接地点外的结点电位

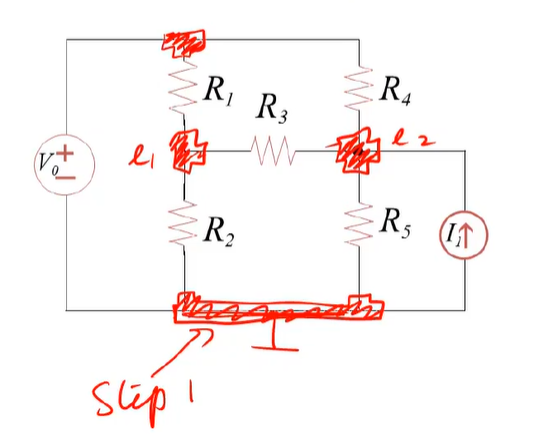
图中最上面的结点的电位可以不用标出，因为它和地之间有一个电压源，所以它的电位大小为$V_0$
可直接记作$V_0$

对每个结点列KCL方程

对$e_1$列KCL：
首先设经过$e_1$的电流都是向外的，画出图来：

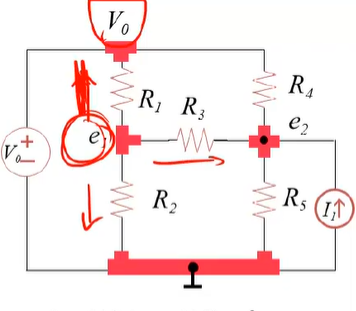
看从$e_1$到$V_0$的电流，由于沿着电流的方向电压减小，而$I=\frac{U}{R}=UG$，所以可以这样表示$I$：

(e_1-V_0)G_1$$。 同理，其他两个电流： $$ (e_1-e_2)G_3

$(e_1-0)G_2$

根据KCL，流入结点的电流等于流出的，流入的为0，流出的已经表示出来了，所以可得：

$(e_1-V_0)G_1+(e_1-e_2)G_3+(e_1-0)G_2=0$

同理可得$e_2$的KCL方程：

$(e_2-e_1)G_3+(e_2-V_0)G_4+(e_2)G_5=I_1$

$流出的=流入的$

求解方程

两个方程，$e_1$和$e_2$是未知数，所以得把两个未知数提出来，常量写到右边（写成$ax_1+bx_2=c$）：

$(G_1+G_2+G_3)e_1-G_3e_2=V_0G_1$

$-G_3e_1+(G_3+G_4+G_5)e_2=I_1+V_0G_4$

写成矩阵形式：

$\begin{bmatrix} G_1+G_2+G_3 & -G_3\\ -G_3 &G_3+G_4+G_5 \end{bmatrix}\begin{bmatrix} e_1 \\ e_2 \end{bmatrix}=\begin{bmatrix} V_0G_1\\ I_1+V_0G_4 \end{bmatrix}$

对于本阶段的题目，直接按中学的求解多元一次方程组的方式求解即可，没有必要使用矩阵的方式求解（1. 求电导矩阵的逆矩阵$A^{-1}=\frac{1}{|A|}A^*$ 2.逆矩阵和电流矩阵相乘得到结果）。

常用的方式

观察上面整理后的方程，可以得出：

$与结点直接相连的电导\times e-与相邻结点相连的电导\times e_{相邻}=流入电流$

所以第3步对每个结点列KCL方程可以直接这么列。
上面的未标出的$e_3$已知，为$V_0$，一般把 $e_3=V_0$ 叫做 增补方程。
其他步骤和上面相同。
注意：当有电压源和电阻串联时，如例题中的$e_1$，那么就可以求出这个支路的电流为$V_0G_1$，方向为电压降低的方向，写在等号右边即可。
当有受控源时，将受控源当成独立源一样对待，即按前面的独立电压源和电流源的方法求解，并添加增补方程：将受控源的控制量用结点电压表示。